On Mathematics and Nightmares
On the road…again!
Afghanistan to Zambia
Chronicles of a Footloose Forester
By Dick Pellek
On Mathematics and Nightmares
Maybe the title of this vignette should be, On Nightmares and Mathematics. As an adult, the Footloose Forester does not have many nightmares, but when they disturb his sleep, most of the unpleasant dreams are about his unpreparedness for taking exams. Exams in the past, happy to say! Or dreams about hypothetical situations in the past that never actually happened. For example, one remembered nightmare was about his unpreparedness to take an exam in microeconomic theory. In the dream, he was registered for the class in night school at Rutgers, but fretted about taking the final exam because he had not studied for the test; indeed he had not even attended the classes except for the first one. Yet, he learned from other students that one final exam problem was likely to be about constructing a non-linear graph. The most worrisome part for him was how to assign relevant data to the prospective problem and then graph the results with calculus. Fortunately, it was only a bad dream.
In his waking hours, he is awful at calculus, so perhaps the fear of being found out is what causes him to avoid letting anybody know how incapable he is. The problem has always been that other branches of mathematics, as well, have also been difficult for him. Yet, as a college student, then as a Graduate Student, he was not only expected to take various courses in mathematics, but was expected to be competent in them. Passing an undergraduate math course was one thing, but Graduate Students were assumed to be brighter, thus more competent in mathematics. He was not and never would be competent in math, particularly in abstract fields such as calculus and Boolean algebra.
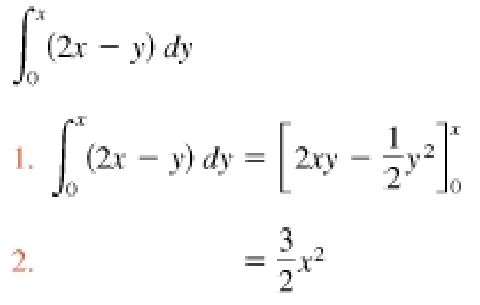
In fact, he cannot even understand most of the equations he created and solved satisfactorily in the past, as part of his studies and dissertation. So the Footloose Forester is ever embarrassed to even mention one of his published works that contains a mathematical description with actual project parameters, because he can no longer explain the steps or solve the equation.
This episode in confessions and soul-searching continues: Once, as a Graduate Student, and fresh out of a course in college algebra and pre-calculus, he was approached by a French Grad Student who asked him about the proper application of the inverse sine. His friend asked because he knew that the Footloose Forester had just completed the class in which inverse sine functions had been covered. It didn’t matter; the Footloose Forester at first didn’t comprehend the mathematical expression, then struggled with explaining how to solve the problem. He clearly remembers telling the Frenchman that, although he had been exposed to formal math instruction very recently, math was simply not part of him. It just does not stick.
Most of the exams he fretted about were some applications of mathematics; and, consequently, most of his nightmares involved trying to solve math problems. Once, he joined a course in Advanced Forest Mensuration in which Matrix Algebra was being applied to inventory problems. The other students had already taken the basic Mensuration course, so they knew enough matrix algebra to cope with the work. The Footloose Forester had to buy a book and learn matrix algebra on his own, in order to keep up with the others because he hadn’t taken the basic course in Mensuration there. There were a few other nightmares about math during those times.
One of those other nightmares he remembers was at the same school, the University of Florida. That nightmare was about a real problem, and it was another one about applied mathematics. In his nightmare, he could not resolve the correct number of variables in the “degrees of freedom” entry for a problem in the Analysis of Variance. Fortunately, he did solve the problem in his sleep, and when his subconscious told him that his answer was correct, he jumped out of bed and went into the dark of night to his laboratory to change his inputs accordingly.
This chronicle is about nightmares and the past and present fear of failing with mathematics. But one of the dreams about math problems was not so haunting to the Footloose Forester, personally. Rather, it was a nighttime re-creation of a mathematical solution offered that very morning by another Graduate Student in a class in Clay Mineralogy at The University of Hawaii. Vince Elder, the Grad Student offering the solution to the professor who taught the class, had graduated with a B.S. in Chemistry. The professor admitted that he did not know of Elder’s approach, so Vince Elder patiently suggested that, in order to quantify the percentage composition of three minerals in a sample, we could use simultaneous equations of three algebraic functions. That is to say, we could solve all three equations at the same time by combining them into one equation. At that stage of his academic development, the Footloose Forester had enough algebra still in his system so that he could actually solve the equations himself. But he also knew that without putting down the problem in his class notebook, he would never be able to do it again.
Vince Elder was such a smart but humble guy, that he took the time to help the Footloose Forester with solving chemical equilibrium problems, as well. Although the typical equilibrium problem required several steps, so that it took up nearly a full page to get to the answer, Vince said (ever so modestly) that he could tell what the answer was going to be by just looking at the original set of equations. The Footloose Forester was always awed by Vince Elder’s intelligence. Mathematics, however, is still the type of nightmare most feared to return.
About the author
Related Posts
Comments 1
Math was a nightmare for me and it was difficult for me to pass exams in this subject. But the more difficult task for me was to write a course paper. I'm glad that my friends showed me ghost writer website and I used the service to complete my task. Now I know what to do when I cannot write a lengthy paper in a short time.




